Abriendo Nuestro Interior: La Geometría Sagrada

“Sobre las representaciones simbólicas, lo importante no es

Lo representado como tal, sino el que se libere lo anímico

De toda muleta física, mediante el proceso de representación”.

(Rudolf Steiner)

Introducción

Convencionalmente, la geometría es una rama de las matemáticas que estudia la lógica de las formas en el espacio, ya sea bidimensional o tridimensional. Es decir, trabaja y explica problemas concretos de la forma. En la vida práctica la geometría presta una gran utilidad para medir las tierras y para poder analizar y comprender las obras concretas que realiza el ser humano (puentes, acueductos, edificios, etc.).

Por otro lado, el término “sagrado” nos sugiere una dimensión espiritual o moral que se inserta en la evolución del ser humano, con una proyección trascendente. Es decir, como lo contrario a lo profano y a la cotidiana practicidad de nuestras vidas.

Si consideramos la unión de ambos aspectos: la dimensión arquetípica de la geometría aplicada a la matemática y la concepción sagrada, nos encontramos con la geometría sagrada que hace referencia a una disciplina en la que se conjugan el aspecto racional y material de la geometría con la concepción intuitiva, espiritual y trascendente. Dejaremos de trabajar únicamente con nuestro hemisferio cerebral izquierdo sobre el que se asienta la lógica matemática, al igual que dejaremos de hacerlo exclusivamente con el derecho que se ocupa de la creatividad y la intuición, para trabajar simultáneamente con ambos hemisferios alcanzando una dimensión holística.

Esta geometría con tintes sagrados es una forma que ha existido mucho antes que la vida apareciera en nuestro planeta y que todos llevamos inscrita en lo más profundo de nuestro subconsciente.

La Geometría Sagrada es un conocimiento que se remonta a los inicios de los tiempos, viene de épocas ancestrales y es probable que no se puedan encontrar sus orígenes, aun cuando se pueden registrar rastros de ésta en diversas civilizaciones, como la Egipcia, la Maya, la Hindú, las comunidades Neolíticas, por mencionar sólo algunas. Las preguntas que surgen son: ¿Qué buscaban aquellos que dejaron las huellas que nos permiten identificar una Geometría Sagrada? ¿Cómo y de quién o de quiénes recibieron este conocimiento?

Desde Platón, pasando por Fra Luca Pacioli, Leonardo da Vinci, Leonardo de Pisa, Matila C. Ghyka, hasta los actuales físicos cuánticos y estudiosos espiritualistas como Drunvalo Melchizedek o artistas como Charles Gilchrist, el artista, matemático y geómetra George W. Hart y muchos otros que nos han permitido ir descubriendo y develando el misterio que hay detrás de la Geometría Sagrada.

Cuando los físicos desarrollaron el microscopio electrónico descubrieron que un mundo de formas geométricas existía en lo infinitamente pequeño. Ya gran número de minerales revelaban a simple vista sus cualidades geométricas y su capacidad de memoria para crearse. Pero mucho antes que el ser humano poblase la Tierra, los astros ya se ordenaban adquiriendo formas esféricas que giraban en elipses, Las galaxias giraban formando inmensas espirales y los cometas se desplazaban en órbitas elípticas. La geometría era algo natural dentro del Universo. La vida tuvo como exponente las cadenas de ADN, auténticas espirales que transmitían información de un ser a otro, incluso muchos moluscos y caracoles adquirieron esta estructura para desarrollar sus caparazones. No nos debe extrañar, por tanto, que las formas geométricas y su simbolismo sean parte de nuestro subconsciente colectivo.

Desde los tiempos más remotos las formas geométricas se convirtieron en símbolos sagrados, místicos, esotéricos y secretos. Algunos de gran poder, otros como manifestación de una religión o corriente esotérica. Todas las tradiciones, religiones y pueblos han considerado estas figuras geométricas como portadoras de un gran simbolismo y poseedoras de un cierto poder mágico.

La enseñanza que nos han dejado nos permite comprender que la Geometría Sagrada es un conocimiento que contiene el patrón de crecimiento, evolución, expansión y desarrollo de todo lo manifestado, lo que, de alguna manera, nos revela los orígenes del tejido del Universo. Como patrón de crecimiento, podemos decir que se trata de una forma abstracta de razonamiento y como tal se puede aplicar no sólo a procedimientos y fenómenos concretos, naturales y empíricos, sino que también a realidades conceptuales, abstractas e incluso espirituales.

En este contexto no se puede dejar de mencionar la estrecha relación que existe entre lo sagrado de la geometría con lo sagrado de los números. Ésta se manifiesta a través de las series numéricas y las relaciones y razones numéricas existentes en las proporciones de las partes componentes de las entidades geométricas, las cuales expondremos más adelante. Podríamos decir que la geometría traza el despliegue de los números en el espacio, realizando un viaje o un camino desde el simple punto, pasando por la línea y llegando al plano, para luego entrar a la tercera dimensión y eventualmente trascenderla, para luego retornar al punto nuevamente. En otras palabras se trata de una disciplina que incursiona en las leyes de ordenación del Universo y de la huella digital de la creación. A través de proporciones, patrones, sistemas, códigos y símbolos, establece las bases tanto de la creación natural (el Universo, la materia, los organismos vivos y su ADN) como de las recreaciones humanas: el arte, la arquitectura, el diseño, la ciencia, la física, la música, la cábala, las matemáticas, etc. A través de estas últimas, el hombre hace de creador e intenta acceder a niveles superiores de consciencia, entendimiento, conocimiento o sensibilidad que lo conecten en forma creciente con la vastedad que lo rodea. Y esto lo logra cuando basa su creación consciente o inconscientemente en la Geometría Sagrada, obteniendo así lo que G.I. Gurdjieff llamaba arte objetivo.

El arte oriental es preciso, matemático, sin manipulaciones. Es una forma de escritura. Por ejemplo, la arquitectura, un edificio de dos habitaciones. Todo aquel que entraba a estas habitaciones, ya fuera viejo o joven, inglés o persa, lloraba; el resultado era siempre el mismo. Con estas combinaciones arquitectónicas, las vibraciones calculadas matemáticamente contenidas en el edificio no podían producir otro efecto. Estamos bajo ciertas leyes y no podemos resistir las influencias externas. Como el arquitecto de este edificio tenía una comprensión diferente y construyó matemáticamente, el resultado era siempre el mismo. Supongamos que llegamos a un monasterio sin ser personas religiosas, pero la música que se escucha en él, nos evoca deseos de orar, sentimientos de paz y recogimiento… Esto sucede porque el arte está basado en leyes.

Esto implica adentrarse en un mundo donde los números se despliegan desde un espacio bidimensional en una superficie plana y luego en un espacio tridimensional. Este proceso ha generado un lenguaje universal cuya carga simbólica trasciendo fronteras y épocas en el tiempo, y es el vínculo axiomático sine qua non para una correspondencia entre lo grande y lo pequeño, el arriba y el abajo, según la Ley de Analogía. Este es el camino de toda realidad manifestada desde su punto inicial de creación hasta su retorno al origen.

Los practicantes de la geomancia se interesan en la Geometría Sagrada porque es el estudio de la manera en que el espíritu se integra a la materia, a través de amplificar y resonar la geometría de la naturaleza y los movimientos planetarios, logramos alinear la resonancia del cuerpo/mente/espíritu con la frecuencia armónica de lo superior y lo inferior. También están interesados en la Geometría Sagrada porque se ha descubierto que ciertos espacios con proporciones especiales, permiten al individuo vibrar en una frecuencia apropiada que le permite maximizar la posibilidad de conexión con el Único.

El Génesis

El Vacío

Antes de comenzar con el primero de los elementos, intentaremos imaginar el espacio vacío, en el cual aún no existe nada y se constituye como el principio de la creación. Es aquel espacio infinito y plenipotencial en el cual se penetra en la meditación cuando logramos acallar la mente y entramos en él, es decir, en el vacío, que es como estar flotando en ninguna parte y que sólo es invadido por una luz blanquecina.

El Punto

En este espacio aparece un simple punto que es el primer arquetipo que conforma la primera dimensión. Éste representa la consciencia de unidad, la mente divina e indivisible. Es donde comenzamos nuestro camino, desde donde iniciaremos nuestra misión para luego retornar al punto que es la raíz absoluta del concepto mental y el que, del mismo modo, es la raíz del pensamiento holístico. Para nosotros es el punto de síntesis que brota del tercer ojo en la glándula hipófisis en el cerebro.

Los Dos Puntos

Del universo unidimensional pasamos al bidimensional donde la unidad se transforma en dualidad. Ocurre este gran milagro y misterio donde el punto aislado se divide y se transforma en dos puntos que dan paso a la segunda dimensión. A partir de esta instancia nos vemos enfrentados a la primera dualidad que genera un espacio medible. Aparece una relación espacial dentro de la cual podemos habitar y desplazarnos.

El Radio y el Arco

Desde el momento que podemos desplazarnos, damos origen a una línea. Es el movimiento entre el primer y segundo punto, es decir la línea recta entre los puntos A y B. Este primer movimiento que se traslada entre estos dos puntos da origen al radio, el cual representa el arquetipo masculino. A continuación se manifiesta un movimiento de rotación donde el punto B gira en torno al punto A configurando el arco, que representa el arquetipo femenino. Es el origen de la dualidad radio/arco de la cual se genera todo camino posterior. Con propiedad podemos llamarlo el movimiento raíz.

A partir de éste se despliega todo el concepto de dualidad: Ying y Yang, luz y oscuridad, izquierda y derecha, arriba y abajo, adelante y atrás, interior y exterior, positivo y negativo, madre y padre, etc. Luego, el juego radio/arco establece todas las energías del universo.

El Círculo

El arco continuará girando a partir del punto B en torno al punto A hasta volver a retornar al punto B desde donde comenzó a girar. Este movimiento da origen a la primera forma cerrada de la Geometría Sagrada. El círculo es una manifestación bidimensional de la Mente Divina e indivisible. Además representa un movimiento y un tiempo que se manifiesta como el primer ciclo cerrado o la primera forma cerrada de la Geometría Sagrada. Es como el ciclo inicial que expresa el Génesis.

Esta relación de desplazamiento en el tiempo del radio/arco se ha expresado en términos matemáticos como Phi, que es la proporción de la circunferencia del círculo con su diámetro. Se trata de un número trascendental o irracional (se verán los números irracionales más adelante), con un valor de 3,14159265. Para propósitos prácticos Phi = 3,1416.

Los números trascendentes son irracionales, pero no todo irracional es trascendente (por ejemplo raíz de 2). Es decir, trascendente implica irracional pero no al revés. El número Phi no sólo es irracional (no es igual a ninguna fracción o cociente de dos enteros) sino que además es trascendente. No es algebraico, es decir no es solución de ninguna ecuación algebraica (=polinominal).

El Rayo y las Seis Direcciones

Nuestra consciencia situada en el centro del espacio puede proyectarse en seis direcciones y por tanto seis rayos. Adelante y atrás, izquierda y derecha y arriba y bajo. Esto lo tenemos que visualizar en el espacio tridimensional. Cabe considerar que para los budistas estas direcciones del espacio pasan a ser diez.

Luego podemos trasladar esta imagen tridimensional a una de dos dimensiones o plana, logrando que estos seis rayos giren y completen el círculo, y a su vez den origen a seis puntos B sobre la circunferencia del círculo. Estos a su vez dan origen a los ejes del patrón de crecimiento de la creación.

Es así como la línea recta o el rayo (arquetipo masculino) en conjunto con la línea curva o arco (arquetipo femenino), dan origen al primer ciclo completo o Génesis que es simbolizado por el primer círculo (bidimensional) o esfera (tridimensional)

Primer Movimiento. Dos círculos de Radio Común

A partir de este círculo (o esfera), se insinúa el primer movimiento, que no hace otra cosa que duplicar esta figura arquetípica, dando origen al primer día después del Génesis. Este segundo círculo se desplaza haciendo centro donde el rayo intercepta el primer círculo originario (punto B). Esta es la primera forma traslapada de la Geometría Sagrada, llamada dos círculos con radio común.

La Vesica Piscis

Este primer movimiento o día del Génesis da origen a la segunda forma cerrada de la Geometría Sagrada: La Vesica Piscis, también conocida como la vejiga del pez o mandorla. Esta forma es como el útero o matriz del universo. A partir de ella se crean todas las formas que se desarrollan en el espacio.

A partir de esta imagen nacen dos nuevos puntos, el C y el D, los cuales se han concebido como los hijos mellizos de A y B. Esta figura también hay que imaginarla en tres dimensiones, en donde las dos esferas dan origen a esta nueva figura tridimensional que es como una pelota de rugby o zeppelín.

Por lo tanto, podemos decir que este primer movimiento del Génesis da origen al patrón de la vida y de la luz, y por tanto, a partir de este momento nuestros ojos pueden ver la creación.

El Segundo Movimiento

El segundo movimiento da origen a un tercer círculo o tercera esfera que representa el segundo día después del Génesis. La relación de estas tres esferas o círculos dan origen a la estrella tetraédrica.

El Tercer Movimiento

Éste da origen al cuarto círculo o esfera que representa el tercer día del Génesis. Si se observan detenidamente veremos que estos cuatro círculos contienen cinco Vesica Piscis y un pétalo central, el cual constituye otra de las figuras contenidas de la Geometría Sagrada.

Estos cuatro círculos son muy simbólicos ya que representan la esencia de la familia en el lenguaje de la Geometría Sagrada. Los círculos 1 y 2 son los padres, los 3 y 4 los hijos, y el corazón de la familia se nos presenta en forma de pétalo.

El Cuarto, Quinto y Sexto Movimiento

Dan origen, respectivamente al quinto, sexto y séptimo círculos o esferas, que a su vez simbolizan el cuarto, el quinto y el sexto día del Génesis.

La Semilla de la Vida

De esta forma, al completar el séptimo círculo, se completa el patrón del Génesis y el principio de la creación del Universo. Es así como se da origen a lo que se conoce como La Semilla de la Vida; y a partir de ésta se concibe el Tubo Toro (llamado simplemente Toro por los matemáticos) o Toroide. Esta es una figura tridimensional que es el resultado de rotar el patrón del Génesis en 360 grados alrededor del centro. Es una esfera que se curva hacia sí misma por arriba o por abajo. Se le suele comparar con una rosquilla, con el anillo de humo de un cigarro o con un neumático o un salvavidas.

Pero al mismo tiempo se puede concebir con un orificio central infinitamente pequeño hacia el cual rotan los círculos componentes, como si fuera un toroide más cerrado.

El Huevo de la Vida

A continuación de la Semilla de la Vida y patrón del Génesis, se produce una segunda rotación hacia el exterior de los seis círculos de esta. Esto se logra haciendo centro en los respectivos cruces de los seis círculos y trazando los próximos seis círculos del mismo tamaño que los anteriores. Luego se borran los primeros seis círculos y se obtiene la silueta del Huevo de la Vida.

El Huevo de la Vida da forma al embrión de la vida humana (a partir de la mórula inicial) y a la morfogenética del cuerpo. El cómo la existencia física de nuestros cuerpos se origina en el Huevo de la Ves materia de un nuevo estudio. En todo caso su carácter embrionario y su forma circular se manifiesta como una cualidad de la geometría femenina, la cual revela las primeras formas geométricas masculinas de carácter angular y en base a tramos rectos. Éstas son el cubo, el tetraedro y la estrella tetraédrica.

La Flor de la Vida

Si observamos la construcción del Huevo de la Vida, veremos que hay seis puntos donde se cruzan tres círculos. Si hacemos centro en cada uno de ellos y trazamos sus respectivas circunferencias en el mismo tamaño que las anteriores, obtendremos una tercera rotación.

Esta tercera rotación permite la construcción de la Flor de la Vida. Son seis círculos azules, seis verdes y seis rojos, más el verde central, que hacen un total de 19 círculos. Es muy importante observar que los seis círculos exteriores azules tocan tangencialmente al círculo verde central. Podemos reproducir esta figura si colocamos siete monedas iguales sobre una mesa.

Estos diecinueve círculos conforman una figura de una gran importancia en la Geometría Sagrada y ha estado presente en las más variadas civilizaciones desde tiempos inmemoriales. Siempre los diecinueve círculos, los cuales fueron rodeados por dos círculos mayores, son los que dieron forma a la Flor de la Vida. A esta altura nos damos cuenta que este patrón podría seguir hasta el infinito, sin embargo se detiene aquí.

El Fruto de la Vida

Al observar este patrón vemos que en el perímetro externo de la figura se insinúan muchos círculos que están incompletos. Si nos aventuramos a completarlos y seguir con este patrón tendremos una cuarta rotación que nos permite continuar con los círculos tangentes hasta llegar a tener trece. Al aislarlos como si colocáramos, igual que lo hicimos antes, monedas del mismo tamaño en forma tangente sobre la mesa, tendremos el Fruto de la Vida.

El Cubo Metatrón

Hasta el momento hemos incursionado principalmente en un patrón femenino, en el cual se ha desplegado una gran cantidad de círculos, los cuales han arribado como una suerte de síntesis, al patrón llamado el Fruto de la Vida, conformado por trece círculos tangentes. Este patrón, en conjunto con el Huevo de la Vida y el Tubo Toro o Toroide, conforma los tres patrones fundamentales de la existencia.

A estos patrones, concebidos por círculos femeninos, se sobreponen líneas rectas masculinas: los sistemas informacionales de la creación.

Así como ocurriera con el Huevo de la Vida, el cual permitió la formación de algunas formas masculinas a partir del punto central de sus círculos, el Fruto de la Vida da origen, al unir los puntos centrales de sus círculos, al Cubo Metatrón, que es la contraparte masculina del Fruto de la Vida, utilizando la energía masculina de las líneas rectas que unen dichos centros y que es uno de los sistemas informativos esenciales de la creación. La correcta construcción del Cubo Metratón se logra trazando un círculo cuyo centro está en el centro del círculo central y su radio coincide con los centros de los círculos exteriores del fruto de la vida (círculo azul). Luego se traza un segundo círculo (verde) con el mismo centro que el azul pero con un radio que es igual al radio del círculo azul multiplicado por Phi de valor 0,6180339.

Luego se traza una estrella tetraédrica haciendo crecer la interior hasta que sus vértices hagan contacto con el círculo interior (verde). Estos puntos indican el trazado que permitirá, a su vez, trazar correctamente el Cubo Metatrón completo, de modo de poder trazar las coordenadas que permiten construir la totalidad de los Sólidos Platónicos, especialmente el dodecaedro y el icosaedro.

Este cubo debe su nombre al ángel Metatrón, el cual también es conocido como el primero y el último de los Arcángeles, y recibe diversas denominaciones como Canciller del Cielo, Ángel de la Alianza y Rey de los Ángeles. Su función celestial es la de supervisar la anotación de todos nuestros actos en el Libro de la Vida.

Los Sólidos Platónicos

Los Sólidos Platónicos son cinco estructuras espaciales que conforman volúmenes tridimensionales en los cuales todas sus caras son de la misma forma y del mismo tamaño y cuyos bordes o aristas tienen la misma longitud. Además todos los ángulos interiores son también del mismo tamaño. Por último, si inscribimos cada Sólido Platónico en una esfera apropiada, todas las puntas tocarán la superficie de la esfera.

Estos Sólidos fueron nominados después que Platón los describiera en el 350 A.C. en su obra “El Timeo”. Han llegado a ser la base de la estructura de la vida orgánica y de las obras de creación humana. Las podemos encontrar en la vida animal y orgánica, en los minerales, en el sonido, en el lenguaje, en la música, en las artes plásticas, en la arquitectura, en las obras de ingeniería, etc.

Los cinco Sólidos Platónicos son:

El Tetraedro, cuyas caras son cuatro triángulos equiláteros iguales. De este poliedro se desprende la estrella tetraédrica, que no es otra cosa que dos tetraedros invertidos e intersectados.

El Cubo o Hexaedro, que es un poliedro cuyas caras son seis cuadrados iguales.

El Octaedro, cuyas caras son ocho triángulos equiláteros iguales.

El Dodecaedro, que es un poliedro de doce caras conformadas por doce pentágonos regulares.

El Icosaedro, que tiene veinte caras conformadas por veinte triángulos.

Si observamos con detenimiento cada uno de estos poliedros trazados en el Cubo Metatrón veremos que tienen una versión igual pero más pequeña que se inscribe en los siete círculos tangentes interiores que se manifestaron en la tercera rotación.

El Árbol de la Vida

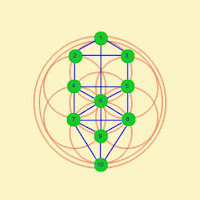
El Árbol de la Vida es el símbolo geométrico que se expresa como la base de la Cábala, que es el antiguo sistema místico del judaísmo. Cada uno de los vértices simboliza una Sephirah, que a su vez representa un atributo de Dios. En esta figura se puede ver la perfecta relación existente entre el Árbol de la Vida y el patrón del Génesis manifestado en la Semilla de la Vida.

Los Sephiroth del Árbol de la Vida

1. Kether (Corona)

2. Binah (Comprensión)

3. Kjokmah (Sabiduría)

4. Gueburah (Poder)

5. Kjesed (Misericordia)

6. Tiphereth (Belleza)

7. Hod (Gloria)

8. Netzach (Victoria)

9. Yesod (Fundación)

10. Malkuth (Reino)

La Cuadratura del Círculo

Como hemos podido ver, el arco o línea curva representan el arquetipo femenino y el radio o línea recta el masculino. La forma cerrada primaria que construye el arco es el círculo, y en el caso de la línea recta es el cuadrado. Por otro lado el círculo ha sido la forma que se le ha asignado a los cielos y el cuadrado a la tierra. Desde muy antiguo se ha intentado equilibrar o unificar el cielo con la tierra, el espíritu con la materia, lo femenino con lo masculino, etc. En otras palabras, asimilar al máximo el perímetro del cuadrado con el del círculo y su circunferencia. Esto es lo que se conoce como la cuadratura del círculo.

Se trata de construir un cuadrado que tenga el mismo perímetro que un círculo dado. O bien el mismo área que un círculo dado. Y resulta que no es posible construirlo usando sólo regla y compás.

Es una tarea que no ha sido fácil y es probable que la respuesta exacta todavía no haya podido encontrarse. La respuesta es que no es posible realizar la construcción con regla y compás, pero por supuesto, existe un cuadrado con la propiedad requerida. Una de las aproximaciones más precisas radica en concebir un cuadrado cuyo lado es igual al diámetro de la Tierra (12.700 Km.). Es decir, la Tierra queda inscrita en un cuadrado de esta medida. En seguida se traza un círculo haciendo centro, en el centro del cuadrado que contiene el círculo de la Tierra y cuyo radio es igual a la suma del radio de la Tierra (6.350 Km.) más el radio de la Luna, cuyo diámetro es 3.500 Km. aproximadamente (1.750 Km), quedando el radio en cuestión en 8.100 Km.

Tenemos entonces el perímetro del cuadrado A-B-C-D:

12.700 x 4 = 50.800 Km.

Y el perímetro de la circunferencia de radio R:

2 x Phi (3,1416) = 6,2832 x r (8.100) = 50.894

Es decir habría un error de un 1,7 %

Por otro lado el conocido dibujo de Leonardo da Vinci de “El hombre de Vitruvio”, construido en la superposición del círculo y el cuadrado, presenta una aproximación un poco más alejada que la anterior a la buscada cuadratura del círculo. En este dibujo el cuadrado tiene como lado 7 unidades y el radio del círculo es de 4,2 unidades.

Por lo tanto:

Perímetro del cuadrado = 7U x 4 = 28 U

Perímetro de la circunferencia = 2 x Phi (3,1416) = 6,2837 x r (4,2 U) = 26,4

Error = 5,7 %

Una tercera aproximación a la cuadratura del círculo se ha construido partiendo de cuatro círculos tangentes cuya suma de diámetros definen el lado del cuadrado que los contiene. Luego, haciendo centro en el cruce de las diagonales del cuadrado y con un radio que se integra al radio de los círculos interiores se traza un círculo exterior que se aproxima a la cuadratura del círculo pero que tampoco es exacta.

Perímetro cuadrado = 5 U x 4 = 20

Perímetro de la circunferencia = 2 x Phi (3,1416) = 6,2832 x r ( 3 U) = 18,85

Error= 5,75%

El Eneagrama

El Eneagrama es un símbolo sagrado cuyos orígenes se han situado en hermandades sufíes y que fue presentado en Occidente por el maestro G. I. Gurdjieff. Este símbolo es una combinación de la Ley de Tres con la Ley de Siete o de la Octava. Sus significados pueden ser múltiples y su análisis requiere de un estudio aparte. En todo caso, podemos mencionar que expresa la ley o patrón de evolución y organización de todos los fenómenos y procesos en los diversos planos de la creación. Si bien en esta ocasión sólo veremos el Eneagrama como una imagen de dos dimensiones, es recomendable, al menos, imaginarlo como una esfera tridimensional por la cual circulan energías que transitan los nueve puntos repartidos regularmente en el círculo base. Es decir, se trata de un patrón dinámico.

En esta ocasión su construcción geométrica se ha realizado a partir del patrón llamado el Fruto de la Vida, partiendo de la extensión de la Flor de la Vida. Primero se han localizado tres ejes de dirección que dividen el patrón mencionado en tres partes iguales. Luego se han ubicado (en azul) los tres círculos exteriores en los extremos de los ejes.

En segunda instancia se ubican (en verde) los círculos tangentes a los azules y entre ellos, y en los centros de los círculos verdes se localizan los puntos que dividen cada uno de los tres tramos en tres subtramos, quedando un total de nueve de ellos. Estos seis puntos son los que marcan el recorrido de la Ley de Siete. Luego, haciendo centro en el punto central del patrón, y radio en los centros de los círculos verdes, se traza la circunferencia (en rojo) que contiene el Eneagrama.

Por último, en los puntos en que la circunferencia de color rojo corta los tres ejes, se encuentran los tres vértices del triángulo equilátero, el tetraedro que marca los puntos 3, 6 y 9 que simbolizan la Ley de Tres. Por otro lado, los puntos 1, 2, 4, 5, 7 y 8 son los que permiten la construcción de la Ley de Siete, cuyo recorrido sigue el orden de 1, 4, 2, 8, 5, 7 y de vuelta al 1.

Esta secuencia nace de la unidad (1) dividida por el total de etapas (7).

Del mismo modo, pero desfasado, resulta al dividir:

1:7 = 0,1428571

2:7 = 0,2857142

3:7 = 0,4285714

4:7 = 0,5714285

5:7 = 0,7142857

6:7 = 0,8571428

El Eneagrama es una figura que generalmente se concibe en dos dimensiones, sin embargo, al hacerlo en tres dimensiones nos amplía considerablemente las proyecciones que sobre él tenemos. En esta figura cada línea se transforma en un círculo y el triángulo conformado por los puntos 3, 6 y 9 se transforma en una pirámide.

La Proporción y la Razón Matemática

No cabe duda de que hay variadas definiciones de belleza y muchas de ellas concuerdan en que la belleza se logra cuando hay armonía en las proporciones. Para comprender el concepto de proporción es recomendable remontarse a los orígenes y recurrir a lo que entendían los griegos por proporción o “canon”.

Entendían que la proporción es la igualdad entre dos razones y la razón matemática se definió como el cociente de dos magnitudes homogéneas, entendiendo como cociente el resultado de la división de dos números.

La proporción es algo que encontramos en la naturaleza tanto como en la creación humana. Cuando éstas llegan a una cierta aproximación o equivalencia, es que se puede hablar de una razón matemática que se expresa en una proporción divina, sagrada y de alcances espirituales. Se trata de una proporción que, manifestándose en la naturaleza, es aprehendida y aplicada en obras humanas. En realidad hay muchas proporciones o razones posibles.

Pero es imposible combinar dos cosas sin una tercera; es preciso que exista entre ellas un vínculo que las una. No hay mejor vínculo que el que hace de sí mismo y de las cosas que une un todo único e idéntico. Ahora bien, tal es la naturaleza de la proporción.

“Pero es imposible combinar dos cosas sin una tercera; es preciso que exista entre ellas un vínculo que las una. No hay mejor vínculo que el que hace de sí mismo y de las cosas que une un todo único e idéntico. Ahora bien, tal es la naturaleza de la proporción”.

(Platón)

“La Geometría tiene dos grandes tesoros: uno el Teorema de Pitágoras; el otro es la división de una línea en una proporción extrema y una media”.

(Kepler)

LA DIVINA PROPORCIÓN

A ti, maravillosa disciplina,

media, extrema razón de la hermosura,

que claramente acata la clausura

viva en la malla de tu ley divina.

A ti, cárcel feliz de la retina,

áurea sección, celeste cuadratura,

misteriosa fontana de mesura

que el Universo armónico origina.

A ti, mar de los sueños angulares,

flor de las cinco formas regulares,

dodecaedro azul, arco sonoro.

Luces por alas un compás ardiente.
Tu canto es una esfera transparente.
A ti, divina proporción de oro.

(Rafael Alberti)

Números Racionales, Irracionales y Trascendentes

Números Racionales

Es un número que puede ser expresado como la razón de dos números enteros, como 1/3 ó 37/22. Todos los números que, cuando son representados en notación decimal o bien se detienen después de un número finito de dígitos o caen en un patrón repetitivo, son números racionales.

Números Irracionales

Un número irracional es aquel que no se puede representar como razón de dos números enteros, y en consecuencia no caen en un patrón repetitivo de ningún tipo cuando se expresan en notación decimal.

Números Trascendentales

Estos son ciertos tipos de números irracionales que se llaman números trascendentales. Al igual que los números irracionales, se definen por lo que no son (no son números racionales), sin embargo los números trascendentales se identifican como tal porque no son otro tipo de números, conocidos como números algebraicos.

Un número trascendental requiere de un número infinito de términos para ser definido con exactitud. Es una manera de pensar en Dios. Hay ecuaciones especiales para derivar a los números trascendentales donde los términos son cada vez más pequeños a medida que se avanza, de modo que se pueden ir agregando para alcanzar algún nivel de precisión requerido, pero el verdadero número no se puede lograr con exactitud. Esa es la belleza de los números trascendentales.

A lo largo de las más diversas civilizaciones y épocas, obras de variadas dimensiones y de profundo contenido han manifestado proporciones a partir de cinco razones matemáticas. Estas son expresadas en números irracionales, es decir que no pueden expresarse como una fracción y cuyo desarrollo decimal consta de infinitas cifras. Si bien estos números son infinitos (en realidad son números finitos y lo que es infinito es el largo de su desarrollo decimal), su equivalencia geométrica se acota en forma precisa. Podemos encontrarlos en obras que van desde las pagodas japonesas, los templos mayas, Stonehenge, las grandes pirámides egipcias, las catedrales góticas, por nombrar sólo algunas; han utilizado estas razones:

Raíz Cuadrada de Dos y el Cuadrado

A partir de un cuadrado de lado 1, trazamos su diagonal la cual lo divide en dos triángulos rectángulos, lo que nos lleva a recurrir nuevamente a Pitágoras y su cálculo de la hipotenusa.

Raíz Cuadrada de Tres. El Cuadrado Extendido y la Vesica Piscis

Al abatir el tramo AD se extiende el tramo AB de valor 1, al tramo AF de valor raíz cuadrada de dos, igual a 1,41421. Esto nos arroja un rectángulo de lado 1 y 1,41421, por lo tanto dos triángulos rectángulos con catetos de estos valores. Aplicamos Pitágoras para conocer el valor de la hipotenusa.

Luego, si trazamos dos círculos con radio común 1 AB, la intersección de éstos genera una Vesica Piscis cuyo lado menor (AB) es 1.

El lado mayor (CD) es igual a la raíz cuadrada de tres.

Al unir los vértices del lado mayor C y D con los vértices del lado menor A y B, se obtienen cuatro triángulos rectángulos, a los que, a través de Pitágoras, podemos conocer el valor del cateto desconocido CE y ED; sumados éstos, nos dan el lado mayor CD de la Vesica Piscis.

Raíz cuadrada de Cinco y el Doble Cuadrado

La diagonal del doble cuadrado de lado 1 nos proporciona dos triángulos rectángulos de catetos 2 y 1 respectivamente. Aplicando Pitágoras obtenemos la dimensión de la hipotenusa y diagonal del doble cuadrado, que es raíz cuadrada de 5.

Phi y la Relación entre el Perímetro de la Circunferencia y su Diámetro

Uno de los misterios que más ha intrigado a la humanidad se relaciona con el círculo, aquella figura geométrica perfecta que representa el reino espiritual. Éste radica en la imposibilidad de resolver con absoluta precisión cuál es la relación que existe entre el diámetro de un círculo y la longitud de su perímetro. Es decir, cuántas veces cabe el diámetro en el largo extendido del perímetro de la circunferencia.

Teniendo un círculo de diámetro 1 de modo que su radio intercepte al eje XY en el punto B, hacemos rodar el círculo en el sentido de los punteros del reloj hasta que el punto B del radio haya dado toda la vuelta e intercepte nuevamente el eje XY. De este modo habremos desplegado el perímetro total de la circunferencia. Esto sucede un poco más allá de haber avanzado tres veces el diámetro del círculo. Este largo se ha definido como Phi, con un valor de número irracional 3,1416.

La Proporción Áurea

La Proporción Áurea es la división armónica de una recta en media y extrema razón. Es decir, que el segmento menor es al segmento mayor, como éste es a la totalidad de la recta.

Ya hemos trabajado con patrones estructurados con el círculo femenino y de éstos se han derivado nuevos patrones a los cuales se les ha sobrepuesto la línea recta masculina. En esta oportunidad trabajaremos con la línea recta en forma independiente, con la finalidad de incursionar en el concepto de la proporción, es decir de la relación entre las partes o magnitudes medibles. Esta relación proviene de cierta razón matemática, detrás de la cual se manifiesta la armonía del mundo que nos rodea. En este sentido debemos comprender que nos enfrentamos a una dimensión sensible de la existencia, más allá de un concepto de perfección abstracto.

Cuando hablamos de proporción, lo estamos haciendo respecto de dimensiones comparadas, por lo tanto de números. La comparación más básica que podemos hacer es relacionar un todo que dividimos en dos partes, lo cual nos arroja tres entidades: Parte a, parte b y una totalidad c. Esto lo aplicaremos a un segmento o línea recta entre los puntos A y B, que denominaremos tramo c, en el cual ubicaremos un punto C, que a su vez dividirá el tramo c en dos subtramos a y b. La relación o proporción más evidente es que el punto C esté ubicado justo al medio del tramo AB, con lo cual tendríamos que a = b y, lógicamente, a+b=c.

Las otras posibilidades son que a sea mayor que b, o que b sea mayor que a.

De acuerdo a Fra Luca Paccoli de Borgo, existe una proporción de origen divino en que la relación de las partes es: a es b, como c es a a. En otras palabras que el tramo AB sea al tramo AC como el tramo AC es al tramo CB. Es decir que el tramo completo sea al subtramo mayor, como éste es al menor.

Una variante interesante es que usemos el punto C para doblar el segmento AB, como si fuera un vara de plomo y lo juntamos con otra igual, para formar un rectángulo. Uno se pregunta entonces, ¿dónde habrá que doblar para que el rectángulo se vea lo más armónico posible? Si se hace el experimento con muchos sujetos, la mayoría opta por una forma de rectángulo cuya razón largo : ancho estará muy cerca de la razón áurea.

Solo hay un punto C que cumple con esta condición, que se manifiesta como la razón que expresa la igualdad a/b = a+b/a, que es lo mismo que a/b = c/a, o bien a2=b(a+b). Esta proporción se reduce a un número que multiplicado por el tramo a me dará el tramo a+b que equivale al tramo c, donde ambos cumplen con la proporción o relación referida. Lo mismo si tomamos el tramo c y lo dividimos por el mismo número obtendremos el valor numérico del tramo a.

Este número es el llamado número áureo o número de oro o simplemente número Phi. Número que encontraremos presente en las bellas artes, en la arquitectura, en las plantas, en el cuerpo humano, en los animales y en todo el Universo.

Construcción de la Proporción Áurea y Obtención de Phi a partir del Cuadrado y del Rectángulo Áureo

Vamos a suponer un tramo a entre los puntos A y C. Le daremos al tramo a un valor de 2 unidades. A partir de este tramo se construye un cuadrado ACDE de lado a con valor 2. A continuación encontramos el punto medio del tramo AC, el cual queda dividido en dos subtramos de 1 unidad. Unimos este punto con el vértice D del cuadrado y con un compás hacemos centro en el mencionado punto medio y arco en D y lo abatimos sobre la prolongación del tramo AC donde lo corta está el punto B. Ahora tenemos el tramo b entre los puntos C y B que queda en proporción áurea en relación al tramo a. A su vez esto permite construir el rectángulo áureo ABFE.

El Pentágono y el Triángulo Áureos

El pentágono regular da origen al triángulo áureo que es un triángulo isósceles con dos ángulos en la base que miden 72 y el ángulo opuesto 36. A su vez, si la base del triángulo mide 1, sus otros dos lados están en proporción áurea y miden 1,6180339…

Luego el pentágono da origen a la estrella de cinco puntas, la que es considerada una figura de gran contenido simbólico. Con una punta hacia arriba se considera una protección contra el mal y al contrario, cuando se ubica con dos puntas hacia arriba, un signo del mal (Pentagramaton), considerado como la supremacía de la materia sobre el espíritu. Además todos sus trazos se encuentran en la proporción áurea. Esto se ve en las relaciones de los trazos A, B, C y D.

En seguida podemos observar la existencia de tres tamaños de triángulos áureos insertos en la estrella de cinco puntas que se inscribe en el pentágono áureo. Cada uno mantiene la misma relación áurea entre la base del triángulo y cada uno de sus otros dos lados.

La Serie Fibonacci y la Proporción Áurea

Para comprender la serie Fibonacci debemos primero definir lo que se entiende por una serie numérica. Esto no es otra cosa que una sucesión progresiva de números que sigue un patrón definido en su evolución. Por ejemplo, la sucesión de números naturales, de números pares, de números impares, de números primos, etc.

No está muy claro cuál es el patrón de los números primos: en realidad parece aleatorio, y la sucesión de los primos contiene secuencias aritméticas arbitrariamente largas (teoremas recientes de Terence Mao, premio Nobel en matemáticas, año 2006).

En el caso de la serie Fibonacci, se trata de una sucesión infinita de números naturales que parten de 0 y luego el 1, para continuar con la suma de los dos anteriores. Por lo tanto, 0+1=1, en seguida se suman los dos últimos, es decir 1+1=2, para seguir con 1+2=3, a continuación 2+3=5, luego 3+5=8 y así hasta el infinito.

Si bien esta serie numérica primero fue descubierta por matemáticos de la India como Gopala alrededor del año 1135 y luego Hemachandra en 1150, que investigaron los patrones rítmicos que se formaban con notas o sílabas, su real dimensión nos ha llegado a Occidente, desde que fuera descrita y explicada por Leonardo de Pisa, también llamado Leonardo Fibonacci, un matemático italiano del siglo XIII.

Leonardo de Pisa la describió con el fin de resolver un problema que planteaba la cría de conejos, tratando de encontrar el patrón rítmico de nacimiento de éstos.

Más adelante fue descrita también por el matemático alemán Johannes Kepler en el siglo XVI. Y luego el matemático escocés Robert Simpson en 1753 descubrió la relación de dos números sucesivos de la serie Fibonacci con la proporción áurea, detectando que mientras más progresan éstos, más se aproxima su cociente al Número de Oro o Divina Proporción.

Tomamos el número inicial 0+1 = al número siguiente que en este caso es 1 y al sumar el 1 inicial con el 1 siguiente tenemos 2, al sumar ambos tenemos 3, luego al sumar estos dos números, llegamos a 5, enseguida a 8, después a 13 y así sucesivamente hasta el infinito. A continuación, si dividimos el número siguiente por el número inicial de cada línea de la serie, nos da un número con infinitos decimales, por razones prácticas los limitaremos a siete decimales, y así encontramos que los resultados se van aproximando paulatinamente al número que hemos descrito como Número Áureo con siete decimales PhiØ = 1,6180339, lo que se logra cuando se llega a la división 6.765/4.181. De ahí en adelante las divisiones que siguen tendrán siempre los mismos primeros 7 decimales hasta el infinito. Si hacemos lo mismo con tres decimales, este número PhiØ = 1,618, se estabiliza a partir de la división 233/144.

En realidad, para cualquier número de decimales que nos demos de antemano, se observa que la sucesión de los cocientes llega a coincidir en esos decimales con el número Phi.

Ahora bien, si hacemos las divisiones a la inversa, es decir, el número inicial dividido por el siguiente, o sea, si en lugar de dividir 10.946/6.765 = 1,6180338, dividimos 6.765/10.946 = 0,6180339. Esto es la Proporción Áurea a la inversa, es decir, si el tramo mayor mide 1 unidad, el tramo Áureo menor medirá 0,6180339.

Esta serie numérica la podemos encontrar en numerosas manifestaciones de la naturaleza:

- La relación entre la cantidad de abejas macho y abejas hembra en un panal.

- La relación entre la distancia entre las espirales del interior “espiralado” de cualquier caracol.

- La relación entre los lados de una estrella de cinco puntas o estrella de David.

- La disposición de los pétalos de las flores (el papel del Número Áureo en la botánica recibe el nombre de Ley de Ludwig).

- La distancia entre las espirales de una piña.

- La relación con el cociente entre el número de espirales horarias y antihorarias de una flor de girasol o maravilla.

- Las relaciones entre muchas partes corporales de los humanos y los animales.

- La relación entre la altura de un ser humano y la altura de su ombligo.

- La relación entre la distancia del hombro a los dedos y la distancia del codo a los dedos.

- La relación entre la altura de la cadera y la altura de la rodilla.

- La relación entre las divisiones vertebrales.

- La relación entre las articulaciones de las manos y los pies.

- Una gran cantidad de creaciones artísticas.

- Relaciones arquitectónicas en las Pirámides de Egipto.

- La relación entre las partes, el techo y las columnas del Partenón, en Atenas (s. V a. C.).

- En los violines, la ubicación de las efes (los oídos, u orificios en la tapa) se relaciona con el Número Áureo.

- El número áureo aparece en las relaciones entre altura y ancho de los objetos y personas que aparecen en las obras de Miguel Ángel, Durero y Da Vinci, entre otros.

- Las relaciones entre articulaciones en el hombre de Vitruvio y en otras obras de Leonardo da Vinci.

- En las estructuras formales de las sonatas de Mozart, en la Quinta Sinfonía de Beethoven, en obras de Schubert y Débussy (estos compositores probablemente compusieron estas relaciones de manera inconsciente).

- Autores como Bártok, Messiaen, Stockhausen compusieron obras cuyas unidades formales se relacionan (a propósito) con el número áureo.

La Espiral Áurea y la Espiral Fibonacci

La espiral es una de las figuras geométricas con mayor carga simbólica que se expresa en la geometría sagrada. Para comenzar estamos viviendo en una espiral, la galaxia. Esta figura que en teoría no tiene ni principio ni fin está presente en todo nuestro entorno natural, cultural y espiritual. Nuestro oído, con el que escuchamos, se desarrolla en forma de espiral, y también lo encontramos en los conos de los pinos, en algunos cuernos animales, en variadas plantas, en las conchas marinas, en el flujo natural del agua que se escurre por un desagüe, en el flujo de aire de los tornados y huracanes, simbolizando los ciclos de evolución de numerosos procesos, etc. Cada vuelta de la espiral representa un ciclo de evolución, ofreciendo una perspectiva cada vez más amplia e inclusiva. Si imaginamos la evolución como un patrón curvo, la espiral implica el concepto de crecimiento de esta evolución. En caso contrario si la curva vuelve al comienzo, nos encontramos atrapados en un proceso regresivo e involutivo.

Para los propósitos de configurar el tema de la geometría sagrada, distinguiremos dos tipos de espirales. Por un lado la espiral logarítmica, que es la que encontramos frecuentemente en la naturaleza y que se caracteriza porque sus brazos se incrementan en progresión geométrica. Luego está la espiral de Arquímedes, cuyos brazos lo hacen con distancias constantes.

Nos centraremos en la espiral logarítmica, cuya construcción se logra a partir del Rectángulo Áureo, cuyo lado menor es 1 y el mayor es 1,6180339. Otra manera de hacerlo es a partir de la serie numérica Fibonacci aplicada a la diagonal de un cuadrado de lado 1 que crece en la secuencia de la serie Fibonacci: 1,1,2,3,5,8,13…

Ambas espirales, si bien al partir tienen un patrón de desarrollo diferente, a medida que van gradualmente creciendo y alejándose de su centro, comienza a desaparecer la diferencia y se igualan cada vez más. Es decir ocurre algo equivalente a lo que ocurre cuando crece la serie Fibonacci, aproximándose cada vez más al Número Áureo. Por otro lado las espirales se dividen en femeninas y masculinas, lo que dice relación con los dos tipos de energías que las construyen. La espiral masculina se expresa a través de las diagonales de los cuadrados que van girando en 90º. Esto ocurre tanto en los cuadrados que dan origen al rectángulo Áureo para la Espiral Áurea, como en la trama de cuadrados que dan origen a la espiral Fibonacci.

La espiral femenina se va construyendo con el arco que queda conformado entre los trazos de estas diagonales y los círculos cuyos radios son el lado de los cuadrados que definen dichas diagonales.

Uno de las manifestaciones más características y evidentes de la espiral áurea es la concha del caracol Nautilus.

La Espiral, el Triángulo y el Pentágono Áureos

Otra manera de trazar la Espiral Áurea es a partir del Triángulo Áureo, con dos ángulos de 72º en la base y uno de 36º en el extremo opuesto que se genera en el pentágono regular. Utilizando líneas paralelas del trazado de dicho triángulo y del pentágono en el cual se inscribe, se logra construir una secuencia de Triángulos Áureos que permiten trazar los círculos con centros en los puntos A, B, C y D, y cuyos arcos conforman esta nueva espiral áurea.

Consideraciones Finales

A pesar de la extensión de este texto, hay que aclarar que cada uno de los temas que se han tocado son solamente el inicio. Se pueden profundizar y desarrollar mucho más allá de lo expuesto aquí.

Lo sagrado puede considerarse como aquello que conecta al fenómeno individual con la creación toda y con su origen. En el caso de la geometría sagrada, se trata de un sistema simbólico específico que nos evidencia un Universo construido con patrones semejantes desde lo más inmenso hasta lo más pequeño, desde lo global hasta lo más íntimo o personal, en una relación de completa correspondencia que nos llama a la reflexión.

La Geometría es sagrada cuando expresa no sólo relaciones o proporciones físicas o abstractas, sino cuando expresa valores eternos referidos a la belleza, la verdad, o la incidencia de la luz sobre las formas (consciencia), en su danza de radio y arco.

Es importante comprender que todos estos temas no sólo deben comprenderse e incrementar la información que tiene nuestro disco duro, sino que debe alcanzar la dimensión de un trabajo práctico. Es decir que partiendo de la información expuesta, se puede comenzar por armarse de un compás, una escuadra, lápiz y papel, e iniciar nuestra propia investigación que nos llevará a transitar por caminos insospechados.

Todo lo que ha sido expuesto puede y debiera imaginarse en tres dimensiones, lo que potencia aún más el significado esencial de lo que hasta ahora se ha visto.

La profundización de esta práctica en cuanto a trabajo de dibujo tiene el potencial de aproximarse a lo que es un proceso de meditación. Un buen ejemplo es el dibujo de los mandalas, que en algunas circunstancias y con una práctica apropiada son un buen medio de introspección e incluso de sanación, al ser instrumentos de re-ligazón entre lo general y lo particular.

Semilla de la vida --> Tercer Día del Génesis --> Vesica Piscis

Flor de la vida --> Cubo Metatrón --> Laberinto de Chartres

Rueda del desierto --> Escudo Amarillo --> Montaña Sagrada

Geometría Fractal, Geometría Sagrada

Las joyas no dejas de ser figuras de geometría espacial, pero además sus formas y colores les confieren un especial valor mágico. Así, se ha dicho que hay joyas malditas, otras esotéricas y poderosas, las hay que transmiten suerte; también hay minerales, como el cuarzo, capaces de vibrar en la misma honda cerebral que un meditador, lo que les permite cierta comunicación. Las joyas simbolizan, en general, los tesoros ocultos del conocimiento y de la verdad. En el budismo, la joya tipifica la sabiduría y la Joya Triple es Buda, el Dharma y el Sangha; entre los jainistas, las tres joyas son la creencia correcta, el conocimiento correcto y la conducta correcta.

Finalmente están los números, esas cifras que sirven para contar las caras de las figuras geométricas y que tienen un simbolismo propio y de gran profundidad. Para muchas tradiciones los números son el origen de todas las cosas y la armonía subyacente del Universo. En la filosofía hermética, el mundo de los números es comparable con el mundo de la razón. Para Pitágoras “todo está dispuesto según los números” y para Aristóteles el número era “el origen y la sustancia de todas las cosas, así como sus efectos y estados”. En la Cábala, los números se convierten en misteriosos, herméticos en la alquimia, reveladores en el esoterismo, mágicos en el sufismo y proféticos en el cristianismo. Al tener en cuenta el valor numérico de las letras, las de los antiguos alfabetos griego y hebreo, sirvieron para operaciones matemáticas y en la antigüedad grecorromana, sus valores numéricos dieron lugar a una infinidad de interpretaciones basadas en el simbolismo de los números, operando en combinaciones con el procedimiento de suma de cifras.